Read Checkpoint File Gaussian

Return to site

Read Checkpoint File Gaussian

Aug 14, 2016 Locating the Read-Write File for a Job. If you did not use%RWF in the original interrupted job to name a read-write file, then you may be able to find the read-write file in the Gaussian scratch directory (specified by the GAUSSSCRDIR environment variable). It will have the default name assigned by Gaussian, which is of the form Gau.
Guess=Read: Reads the initial guess from the checkpoint file. If the basis set specified is different from the basis set used in the job which generated the checkpoint file, then the wave function.
The surface data may be generated from a Gaussian checkpoint file or be read in from a cube file. Note that there are two steps involved in actually displaying a surface: Obtaining a cube by generating it or reading it in. Generating the actual surface for display.
Guess=Read: Reads the initial guess from the checkpoint file. If the basis set specified is different from the basis set used in the job which generated the checkpoint file, then the wave.
 Next:The Integrals-With-Labels Library Up:The Checkpoint File Library Previous:InitializationContents
Functions for reading information from the checkpoint filechar *file30_rd_corr_lab()
Reads in a label from file30

which describes thewavefunction used to get the correlated energy which is stored infile30 (see file30_rd_ecorr()).Arguments:takes no arguments.
Returns:a string, like 'CISD', or 'MCSCF' orsome other wavefunction designation.

char *file30_rd_label()
Reads the main file30 label.Arguments:takes no arguments.
Returns:calculation label.

char *file30_rd_sym_label()
Reads the label for the point group.Arguments:takes no arguments.
Returns:point group label.
Functions that return char**
char **file30_rd_irr_labs()
Read in the symmetry labels for all irreps in thepoint group in which the molecule is considered.Arguments:takes no arguments.
Returns:an array of labels (strings) which denotethe irreps for the point group in which the molecule is considered,_regardless_ of whether there exist any symmetry orbitals whichtransform as that irrep.

char **file30_rd_hfsym_labs()
Read in the symmetry labels _only_ for those irrepswhich have basis functions.Arguments:takes no arguments.
Returns:an array of labels (strings) which denotethe irreps which have basis functions (in Cotton ordering). For DZ orSTO-3G water, for example, in symmetry, this would be an array ofthree labels: 'A1', 'B1', and 'B2'.
int file30_rd_iopen()
Reads in the dimensionality (up to a sign) of ALPHA and BETA vectors of two-electron coupling coefficients for open shells. (see file30_rd_ccvecs())Note : iopen = MM * (MM + 1), where MM is the total number ofirreps containing singly occupied orbitals.Arguments:takes no arguments.
Returns:the +/- dimensionality of ALPHA and BETA vectors of coupling coefficients for open shells.

int file30_rd_max_am()
Reads in the maximum orbital quantum number of AOs in the basis.Arguments:takes no arguments.
Returns:the maximum orbital quantum number of AOs in the basis.

int file30_rd_mxcoef()
Reads the value of the constant mxcoef.Arguments:takes no arguments.
Returns:the sum of the squares of the number of symmetryorbitals for each irrep. This gives the number of elements in thenon-zero symmetry blocks of the SCF eigenvector. For STO-3G watermxcoef.

int file30_rd_nao()
Reads in the total number of atomic orbitals (read: Cartesian Gaussian functions).Arguments:takes no arguments.
Returns:total number of atomic orbitals.

int file30_rd_natom()
Reads in the total number of atoms.Arguments:takes no arguments.
Returns:total number of atoms.

int file30_rd_ncalcs()
Reads in the total number of calculations (always 1).Arguments:takes no arguments.
Returns:total number of calculations in file30.

int file30_rd_nirreps()
Reads in the total number of irreducible representationsin the point group in which the molecule is being considered.Arguments:takes no arguments.
Returns:total number of irreducible representations.

int file30_rd_nmo()
Reads in the total number of molecular orbitals (may be differentfrom the number of basis functions).Arguments:takes no arguments.
Returns:total number of molecular orbitals.

int file30_rd_nprim()
Reads in the total number of primitive Gaussian functions (only primitives of _symmetry independent_ atoms are counted!).Arguments:takes no arguments.
Returns:total number of primitive Gaussian functions.

int file30_rd_nshell()
Reads in the total number of shells. For example, DZP basis set for carbon atom (contraction scheme ) has a total of 15 basis functions, 15 primitives, and 7 shells. Shells of _all_ atoms are counted(not only of the symmetry independent; compare file30_rd_nprim).Arguments:takes no arguments.
Returns:total number of shells.

int file30_rd_nso()
Reads in the total number of symmetry-adapted basis functions (read:Cartesian or Spherical Harmonic Gaussians).Arguments:takes no arguments.
Returns:total number of SOs.

int file30_rd_nsymhf()
Reads in the total number of irrepsin the point group in which the molecule is being considered whichhave non-zero number of basis functions. For STO-3G or DZ water, forexample, this is three, even though nirreps is 4 (compareint file30_rd_nirreps()).Arguments:takes no arguments.
Returns:total number of irreducible representationswith a non-zero number of basis functions.

int file30_rd_num_unique_atom()
Reads in the number of symmetry unique atoms.Arguments:takes no arguments.
Returns:number of symmetry unique atoms.

int file30_rd_num_unique_shell()
Reads in the number of symmetry unique shells.Arguments:takes no arguments.
Returns:number of symmetry unique shells.

int file30_rd_phase_check()

which describes thewavefunction used to get the correlated energy which is stored infile30 (see file30_rd_ecorr()).Arguments:takes no arguments.
Returns:a string, like 'CISD', or 'MCSCF' orsome other wavefunction designation.

char *file30_rd_label()
Reads the main file30 label.Arguments:takes no arguments.
Returns:calculation label.

char *file30_rd_sym_label()
Reads the label for the point group.Arguments:takes no arguments.
Returns:point group label.
Functions that return char**
char **file30_rd_irr_labs()
Read in the symmetry labels for all irreps in thepoint group in which the molecule is considered.Arguments:takes no arguments.
Returns:an array of labels (strings) which denotethe irreps for the point group in which the molecule is considered,_regardless_ of whether there exist any symmetry orbitals whichtransform as that irrep.

char **file30_rd_hfsym_labs()
Read in the symmetry labels _only_ for those irrepswhich have basis functions.Arguments:takes no arguments.
Returns:an array of labels (strings) which denotethe irreps which have basis functions (in Cotton ordering). For DZ orSTO-3G water, for example, in symmetry, this would be an array ofthree labels: 'A1', 'B1', and 'B2'.
int file30_rd_iopen()
Reads in the dimensionality (up to a sign) of ALPHA and BETA vectors of two-electron coupling coefficients for open shells. (see file30_rd_ccvecs())Note : iopen = MM * (MM + 1), where MM is the total number ofirreps containing singly occupied orbitals.Arguments:takes no arguments.
Returns:the +/- dimensionality of ALPHA and BETA vectors of coupling coefficients for open shells.

int file30_rd_max_am()
Reads in the maximum orbital quantum number of AOs in the basis.Arguments:takes no arguments.
Returns:the maximum orbital quantum number of AOs in the basis.

int file30_rd_mxcoef()
Reads the value of the constant mxcoef.Arguments:takes no arguments.
Returns:the sum of the squares of the number of symmetryorbitals for each irrep. This gives the number of elements in thenon-zero symmetry blocks of the SCF eigenvector. For STO-3G watermxcoef.

int file30_rd_nao()
Reads in the total number of atomic orbitals (read: Cartesian Gaussian functions).Arguments:takes no arguments.
Returns:total number of atomic orbitals.

int file30_rd_natom()
Reads in the total number of atoms.Arguments:takes no arguments.
Returns:total number of atoms.

int file30_rd_ncalcs()
Reads in the total number of calculations (always 1).Arguments:takes no arguments.
Returns:total number of calculations in file30.

int file30_rd_nirreps()
Reads in the total number of irreducible representationsin the point group in which the molecule is being considered.Arguments:takes no arguments.
Returns:total number of irreducible representations.

int file30_rd_nmo()
Reads in the total number of molecular orbitals (may be differentfrom the number of basis functions).Arguments:takes no arguments.
Returns:total number of molecular orbitals.

int file30_rd_nprim()
Reads in the total number of primitive Gaussian functions (only primitives of _symmetry independent_ atoms are counted!).Arguments:takes no arguments.
Returns:total number of primitive Gaussian functions.

int file30_rd_nshell()
Reads in the total number of shells. For example, DZP basis set for carbon atom (contraction scheme ) has a total of 15 basis functions, 15 primitives, and 7 shells. Shells of _all_ atoms are counted(not only of the symmetry independent; compare file30_rd_nprim).Arguments:takes no arguments.
Returns:total number of shells.

int file30_rd_nso()
Reads in the total number of symmetry-adapted basis functions (read:Cartesian or Spherical Harmonic Gaussians).Arguments:takes no arguments.
Returns:total number of SOs.

int file30_rd_nsymhf()
Reads in the total number of irrepsin the point group in which the molecule is being considered whichhave non-zero number of basis functions. For STO-3G or DZ water, forexample, this is three, even though nirreps is 4 (compareint file30_rd_nirreps()).Arguments:takes no arguments.
Returns:total number of irreducible representationswith a non-zero number of basis functions.

int file30_rd_num_unique_atom()
Reads in the number of symmetry unique atoms.Arguments:takes no arguments.
Returns:number of symmetry unique atoms.

int file30_rd_num_unique_shell()
Reads in the number of symmetry unique shells.Arguments:takes no arguments.
Returns:number of symmetry unique shells.

int file30_rd_phase_check()
Reads the phase flag???Arguments:takes no arguments.
Returns:flag.
int file30_rd_ref()
Reads the reference type from the flag in file30.0 = RHF, 1 = UHF, 2 = ROHF, 3 = TCSCF.Arguments:takes no arguments.
Returns:flag indicating the reference.
int file30_rd_rottype()
Reads the rigid rotor type the molecule represents.0 = asymmetric, 1 = symmetric, 2 = spherical, 3 = linear, 6 = atom.Arguments:takes no arguments.
Returns:rigid rotor type.
Functions that return int*
int *file30_rd_am2canon_shell_order()
Reads in the the mapping array from the angmom-orderedto the canonical (in the order of appearance) list of shells.Arguments:takes no arguments.
Returns:an array nshell long that maps shells from the angmom-orderedto the canonical (in the order of appearance) order.
file30_rd_atom_position()
Reads in symmetry positions of atoms.Allowed values are as follows:1 - atom in a general position
2 - atom on the c2z axis
4 - atom on the c2y axis
8 - atom on the c2x axis
16 - atom in the inversion center
32 - atom in the sigma_xy plane
64 - atom in the sigma_xz plane
128 - atom in the sigma_yz plane
This data is sufficient to define stabilizers of the nuclei.Arguments:takes no arguments.
Returns:an array of symmetry positions of atoms.

int *file30_rd_clsdpi()
Reads in an array which has an element for each irrep of thepoint group of the molecule (n.b. not just the oneswith a non-zero number of basis functions). Each elementcontains the number of doubly occupied MOs for that irrep.Arguments:takes no arguments.
Returns:the number of doubly occupied MOs per irrep.

int *file30_rd_openpi()
Reads in an array which has an element for each irrep of thepoint group of the molecule (n.b. not just the oneswith a non-zero number of basis functions). Each elementcontains the number of singly occupied MOs for that irrep.Arguments:takes no arguments.
Returns:the number of singly occupied MOs per irrep.

int *file30_rd_orbspi()
Reads in the number of MOs in each irrep.Arguments:takes no arguments.
Returns:the number of MOs in each irrep.

int *file30_rd_shells_per_am()
Reads in the number of shells in each angmom block.Arguments:takes no arguments.
Returns:the number of shells in each angmom block.

file30_rd_sloc()
Read in an array of pointers to the first AOfrom each shell.Arguments:takes no arguments.
Returns:Read in an array nshell long of pointers tothe first AO from each shell.

file30_rd_sloc_new()
Read in an array of pointers to the first basisfunction (not AO as file30_rd_sloc does)from each shell.Arguments:takes no arguments.
Returns:an array nshell long of pointers tothe first basis function from each shell.

int *file30_rd_snuc()
Reads in an array of pointers to the nuclei on which shells are centered.Arguments:takes no arguments.
Returns:an array nshell long of pointers to the nuclei on which shellsare centered.
int *file30_rd_snumg()
Reads in array of the numbers of the primitiveGaussians in the shells.Arguments:takes no arguments.
Returns:an array nshell long of the numbers of the primitive Gaussians in shells.

int *file30_rd_sprim()
Reads in pointers to the first primitivefrom each shell.Arguments:takes no arguments.
Returns:an array nshell long of pointers to the first primitive from each shells.

file30_rd_sopi()
Read in the number of symmetry-adapted basis functions in each symmetry block.Arguments:takes no arguments.
Returns:an array nirreps long of the numbers ofsymmetry orbitals in symmetry blocks.

int *file30_rd_stype()
Reads in angular momentum numbers ofthe shells.Arguments:takes no arguments.
Returns:Returns an array nshell long ofthe angular momentum numbers of the shells.

int *file30_rd_symoper()
Read in the mapping array between 'canonical' orderingof the symmetry operations of the point group and theone defined in symmetry.h.Arguments:takes no arguments.
Returns:a mapping array nirrep long
int *file30_rd_ua2a()
Read in the mapping array from the symmetry-unique atom list to the full atom list.Arguments:takes no arguments.
Returns:a mapping array num_unique_atom long
int *file30_rd_us2s()
Read in the mapping array from the symmetry-unique shell listto the full shell list.Arguments:takes no arguments.
Returns:a mapping array num_unique_shell long
int **file30_rd_ict()
Reads the transformation properties of the nucleiunder the operations allowed for the particular symmetry point groupin which the molecule is considered.Arguments:takes no arguments.
Returns:a matrix of integers. Each row correspondsto a particular symmetry operation, while each column corresponds toa particular atom. The value of ict[2][1], then, should be interpretedin the following manner: application of the third symmetry operation of the relavant point group, the second atom is placed in the locationoriginally occupied by the atom number ict[2][1].

int **file30_rd_shell_transm()
Reads in the transformation matrix for the shells. Each row of the matrix is the orbit of the shell under symmetry operations of the point group.Arguments:takes no arguments.
Returns:a matrix of nshell*nirreps integers.
Functions that return double
double file30_rd_ecorr()
Reads in the correlation energy stored in file30. To get someinformation (a label) on the type of correlated wavefunctionused to get this energy, see file30_rd_corr_lab().Arguments:takes no arguments.
Returns:the correlation energy.

double file30_rd_enuc()
Reads in the nuclear repulsion energyArguments:takes no arguments.
Returns:the nuclear repulsion energy.

double file30_rd_eref()
Reads in the reference energy (may be different from HF energy).Arguments:takes no arguments.
Returns:the reference energy.

double file30_rd_escf()
Reads in the SCF HF energy.Arguments:takes no arguments.
Returns:the SCF HF energy.
double *file30_rd_evals()
double *file30_rd_alpha_evals()
double *file30_rd_beta_evals()
Reads in the (spin-restricted HF, UHF, and UHF) eigenvalues:the orbital energies.Arguments:take no arguments.
Returns:an array of _all_ of the SCF eigenvalues,ordered by irrep, and by increasing energy within each irrep.(i.e. for STO-3G water, the four eigenvalues all come first, andthose four are ordered from lowest energy to highest energy,followed by the single eigenvalue, etc. -- Pitzer ordering)

double *file30_rd_exps()
Reads in the exponents of the primitive Gaussian functions.Arguments:takes no arguments.
Returns:an array of doubles.

double *file30_rd_zvals()
Reads in nuclear charges.Arguments:takes no arguments.
Returns:an array natom long of nuclear charges (as doubles).
Functions that return double**
double **file30_rd_blk_scf(int irrep)
double **file30_rd_alpha_blk_scf(int irrep)
double **file30_rd_beta_blk_scf(int irrep)
Reads in a symmetry block of the (RHF, UHF, UHF) eigenvector.Arguments:int irrep, designates the desired symmetry block
Returns:a square matrix has orbspi[irrep]rows. The eigenvectors are stored with the column index denoting MOs and the row index denoting SOs: this means that scf_vector[i][j] is the contribution of the th SO to the th MO.

double **file30_rd_ccvecs()
Reads in a matrix rows of which are ALPHA (ccvecs[0]) and BETA (ccvecs[1]) matrices of couplingcoefficients for open shells stored in lower triangular form.Coupling coefficients are defined NOT as in C.C.J.Roothaan Rev. Mod. Phys. 32, 179 (1960) as it is stated in themanual pages for CSCF, but according to Pitzer (no reference yet)and are **different** from those in Yamaguchi, Osamura, Goddard, andSchaefer's book 'Analytic Derivative Methods in Ab Initio MolecularElectronic Structure Theory'.
The relationship between the Pitzer's and Yamaguchi's conventions is as follows : ALPHA = 1-2*a , BETA = 1+4*b , where a and b are alpha's and beta's for open shells defined on pp. 69-70 of Dr. Yamaguchi's book.Arguments:takes no arguments.
Returns:double **ccvecs, a matrix 2 by abs(iopen) rows of which are couplingcoefficient matrices for open-shells in packed form.For definition of iopen see file30_rd_iopen().

file30_rd_contr_full()Read Checkpoint File Gaussian Free
Reads in the normalized contraction coefficients.Arguments:takes no arguments.
Returns:a matrix MAXANGMOM (a constant defined in file30_params.h)by the total number of primitives nprim;each primitive Gaussian contributes to only one shell (and onebasis function, of course), so most of these values are zero.

double **file30_rd_geom()
Reads in the cartesian geometry.Arguments:takes no arguments.
Returns:The cartesian geometry is returned as a matrixof doubles. The row index is the atomic index, and the column is thecartesian direction index (x=0, y=1, z=2). Therefore, geom[2][0]would be the x-coordinate of the third atom.

file30_rd_lagr()
file30_rd_alpha_lagr()
file30_rd_beta_lagr()
Reads in an (RHF, UHF, UHF) Lagrangian matrix in MO basis.Arguments:takes no arguments.
Returns:a matrix nmo by nmo.

double **file30_rd_scf()
double **file30_rd_alpha_scf()
double **file30_rd_beta_scf()
Reads in the (RHF, UHF, UHF) eigenvector.Arguments:takes no arguments.
Returns:a square matrix of dimensions nmoby nmo (see: file30_rd_nmo()).The symmetry blocks of the SCF vector appearon the diagonal of this matrix.

file30_rd_schwartz()
Reads in the table of maxima of Schwartz integrals (ij|ij)for each shell doublet.Arguments:takes no arguments.
Returns:NULL if no table is present in the checkpoint file,a matrix nshell by nshell otherwise.

file30_rd_usotao_new()
Reads in an AO to SO transformation matrix.Arguments:takes no arguments.
Returns:a nso by nao matrix of doubles.

file30_rd_usotbf()
Reads in a basis function to SO transformation matrix.Arguments:takes no arguments.
Returns:a nso by nso matrix of doubles.
The z-matrix is read from file30 as an array of z_entry structswhich are declared in file30.h. This structure contains the reference atom,an optimization flag, the coordinate value, and any label used for each internal coordinate. When not applicable (such as the first few lines of a z-matrix) atom variables are given values of -1,opt variables are given values of -1, val variables aregiven values of -999.9, and label strings are left empty. 
file30_rd_zmat()
Reads in the z-matrixArguments:takes no arguments.
Returns:struct*z_entry natom long.

 Next:The Integrals-With-Labels Library Up:The Checkpoint File Library Previous:InitializationContentsRead Checkpoint File Gaussian ToolMicah Abrams2001-11-02Joseph W. Ochterski, Ph.D.
help@gaussian.com
June 21, 2000
Abstract:The purpose of this paper is to describe how to use GaussView (or GaussViewW) to create jobs and visualize results calculated by Gaussian, when Gaussian is installed on a different computer (running Unix).
ContentsOverview
Introduction
There are a variety of reasons you may want to run GaussView and Gaussian on different computers. The typical reason is that the computer with Gaussian has more resources – memory, disks or processors. Throughout the rest of this document, I'll refer to the machine running GaussView (if it's a Unix computer) or GaussViewW (if it's running Windows) as the local machine, and the Unix machine on which Gaussian will run as the remote machine. Also, I'll use GaussView as short had to mean 'GaussView on a Unix machine, or GaussViewW on a Windows machine.'
The ShortcutFor those who don't want to read the entire document, I'll give a sneak peek at the essential point here; the rest of the document will be a description of how to create formatted checkpoint files and how to use them. GaussView gets results from Gaussian via formatted checkpoint files and log files (i.e. Gaussian output files). If you already know how to generate formatted checkpoint files and move them around, then you needn't read further. If you didn't understand all that, don't worry, I'll explain it below.
OverviewThe whole process of creating jobs, running them, and visualizing the results can be broken down into five essential steps:
Create the input file.
Transfer the input file to the remote computer.
Run the calculation and prepare the output file.
Transfer the output file(s) back to the local computer.
View the results.
The next few sections describe these steps in detail. How to mineshafter on mac. First, though, I'll give a brief list of some assumptions I've made about how things (computers and software) are set up.
I'll assume the local machine has the following:
GaussView is installed if it is a Unix machine; GaussViewW is installed if it is running Windows.
Either Gaussian or the Gaussian utilities are installed. Technically, it is possible to generate cube files on the remote machine and view them on the local machine, but I will not discuss that process in detail.
The machine should be hooked up to a network, and should be able to run network software such as ftp and telnet.
The assumptions for the remote machine are similar:
It should be a Unix-type system, so users can log in.
Gaussian should be installed, and be accessible for users. This includes setting up the initialization files, as described in the Gaussian User's Reference.
You have an account and password on the Unix system.
It has a network connection. As for the local system, ftp should be available to users.
Step 1: Create an input fileThis can be as simple as firing up GaussView, building your molecule, and saving it as an input file (.com or .gjf). However, if you are interested in visualizing surfaces (electrostatic potential, orbitals, density, etc.), then there will be an additional step you need to take before you save the input file; namely, indicating in the input file that you wish to save a formatted checkpoint file. By formatted, I mean human readable, rather than binary.
GaussView needs to read in formatted checkpoint files, which generally have the extensions .fch or .fchk, in order to have enough information to be able to calculate surfaces. Gaussian does not generate these files by default, but will generate them if the input file indicates that it should.
Modifying an input file is a straight forward procedure, and can be done within GaussView, from the Gaussian Calculation Setup window. To see that window, from the GaussView main menu, choose Calculate->Gaussian.., and the Gaussian Calculation Setup window will pop up. Exactly what to do in that window is described below. When you've made your modifications, you can save them in a file by clicking on the Retain button in the Gaussian Calculation Setup window, then choosing File->Save.. from the GaussView main menu. Save it with file type 'Gaussian,' with either a .com or .gjf extension. Gaussian accepts both .gjf and .com files equivalently as input. Remember the name of the file and the directory you saved it in, you'll need to know these later.
The easiest way to tell Gaussian to generate a formatted checkpoint file is to add the keyword FORMCHECK to the 'Additional Keywords' box in the Gaussian Calculation Setup window. This tells Gaussian to create a formatted checkpoint file named Test.FChk when the job completes successfully. If the job fails, Test.FChk will not be created. The name of the file will always be Test.FChk. If you need the additional flexibility of a checkpoint file with a different name, then you can simply rename it after the calculation finishes.
There is another way, which is somewhat more flexible, to generate a formatted checkpoint file. If you modify your input file so that it has a %chk card (which is described in Chapter 2 of the Gaussian User's Reference), then Gaussian will not delete the unformatted checkpoint file after the calculation has completed. You can format this checkpoint file using Gaussian‘s formchk utility. Instructions for doing this are included in section 3.3, 'Step 3. Run the calculation.' You do not need to use the FORMCHECK keyword. If you do, then both the unformatted checkpoint file and Test.FChk will be available at the end of the calculation.
Step 2: Transfer the input file to the remote computerNow that you've saved the input file, you need to transfer it to the remote computer so Gaussian can use it. One way to do this is to use ftp, which is included with Windows, and is available on most Unix machines. Here are the steps to take to transfer the file:
Get a command prompt.Windows: From the Windows task bar (the one on the bottom of the Windows screen), click Start->Programs->Command Prompt, and a command prompt window will pop up.
Unix: Hopefully, an xterm, or it's equivalent is already running. If GaussView is running in the xterm, you can either exit GaussView, or make it a background process by typing Ctrl-Z, then bg at the prompt.
Change directories on the local machine. Change directories (using the cd command) to the directory on the local machine where you saved your input. Remember that on Windows machines, the slashes point the opposite way from Unix machines (Windows: ; Unix: /).
Start ftp. Type ftp machine where machine is the name (or IP address) of the remote machine where you'll run the Gaussian calculation. When ftp asks for them, enter your username and password.
Change directories on the remote machine. With ftp, use the cd command to the directory where you want the input file to go on the remote machine (remembering the different Unix/Windows slash conventions:(Windows: ; Unix: /).
Copy the input file to the remote machine. Once you are in ftp, connected to the remote machine, and in the proper directory there, you can copy the input file to that machine using ftp's put command, like this: put name.gjf. The file will then be copied to the remote machine.
Quit from ftp. That's it – now you can leave ftp using the quit command.
Step 3. Run the calculation For this step, you need to be connected to a command prompt on the remote machine. Typically the telnet program is used to do this.
Log into the remote machine. Again, you'll need your username and password. Type telnet machine, where machine is the same computer you ftp'd the file to, and enter your username and password when prompted.
Change directories. Use the cd command to change directories to the directory you put the file in on the remote machine.
Run the job. How you actually do this depends a bit on how Gaussian was set up on the remote computer. Generally, you can run Gaussian as described in the Gaussian User's Reference; however, on computers which use batch queues, you'll have to contact your administrator to find out how to run Gaussian if you don't already know. If your remote machine does use queues, you may have to modify the script you submit to the queue to make it copy the Gaussian log file and the Test.FChk file to a safe place until you copy them to the local machine.Once the job has successfully finished, you can rename the Test.FChk file, if you wish to, using the Unix mv command. Generally, formatted checkpoint files have the extension .fchk (.fch on Windows). Using this extension will make it somewhat more convenient to load the file into GaussView. Warning: if you choose not to rename it, remember that you may accidentally overwrite an older Test.FChk file when you run another job using the FORMCHECK keyword.
If you did not use the FORMCHECK keyword, but chose to use a %chk card, then you need to take the extra step of formatting the checkpoint file now, so that GaussView can read it. The formchk utility, which is part of Gaussian, is the correct tool for doing this. Just type: formchk name.chk, and formchk will create name.fchk. This is just one way to use formchk; other ways are described in the Gaussian User's Reference.
Exit from telnet. If your job is a long running one, you may which to exit from telnet, and come back from time to time to check on it. If it's a short one, you can check to make sure it has completed successfully, and then exit. You may leave telnet with the exit command.
Step 4. Copy the output files back to the local machine.This is essentially the same process as moving the input file to the remote machine.
Get a command prompt.
Change directories on the local machine. Change directories to the directory on the local machine where you want the output to end up.
Start ftp.
Change directories on the remote machine. Again, use the cd command to the directory where the output files are.
Copy the output file(s) from the remote machine. You can copy the output file(s) from the remote machine using ftp's get command, like this: get input.log or get input.fchk. The files will then be copied from the remote machine.The formatted checkpoint file and the log (.log) file hold slightly different (but overlapping) information. Here's a brief summary of what is in each (as of Gaussian98 Revision A.9), assuming the appropriate calculation was run for that type of information.
Quit from ftp.
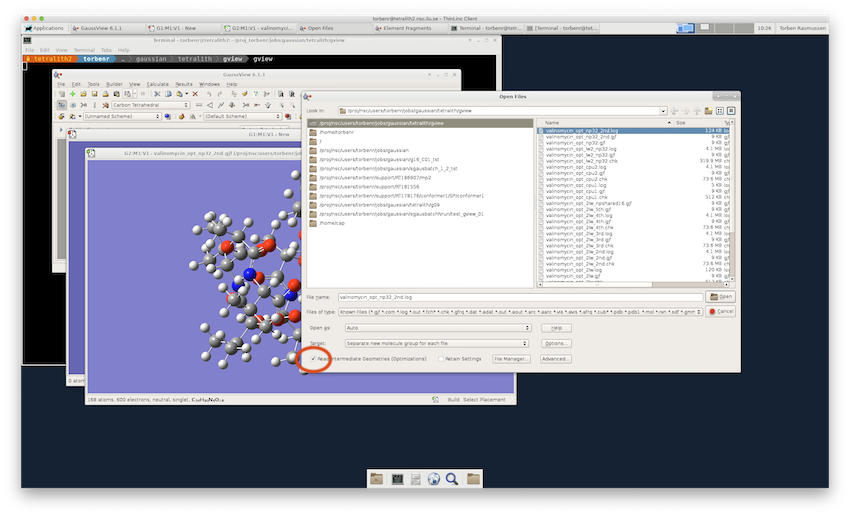
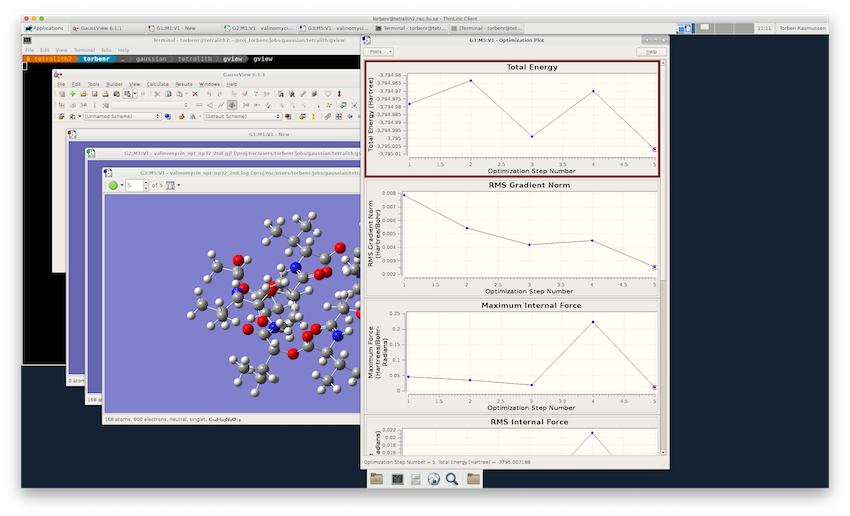
Step 5. View the results.If it's not already running, start up GaussView again. Then select File->Open.. and after selection the corresponding file type, enter either the log file or formatted checkpoint file name in the  Open File window. You may need to change directories in Open File window to find your output files. Once you click Open, the molecule you ran the calculation on will appear in the main GaussView window.
About this document…Visualizing Results when GaussView and Gaussian are Installed on Different Machines
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html remote.
The translation was initiated by Joseph Ochterski on Wed Jun 21 12:22:13 EDT 2000
Copyright © 2000, Gaussian, Inc.
 Author: Joseph Ochterski
 Wed Jun 21 12:22:13 EDT 2000
Last updated on: 21 June 2016.

Arguments:	takes no arguments.
Returns:	a string, like 'CISD', or 'MCSCF' orsome other wavefunction designation.

Arguments:	take no arguments.
Returns:	an array of _all_ of the SCF eigenvalues,ordered by irrep, and by increasing energy within each irrep.(i.e. for STO-3G water, the four eigenvalues all come first, andthose four are ordered from lowest energy to highest energy,followed by the single eigenvalue, etc. -- Pitzer ordering)

Arguments:	int irrep, designates the desired symmetry block
Returns:	a square matrix has orbspi[irrep]rows. The eigenvectors are stored with the column index denoting MOs and the row index denoting SOs: this means that scf_vector[i][j] is the contribution of the th SO to the th MO.